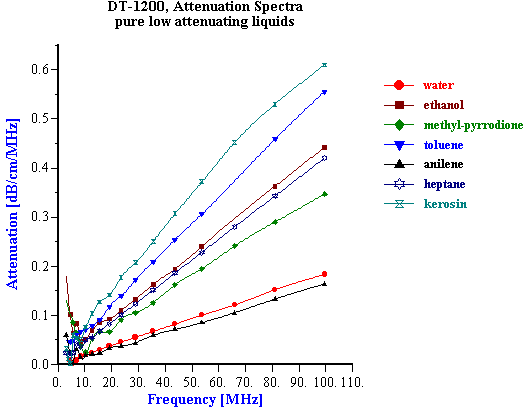
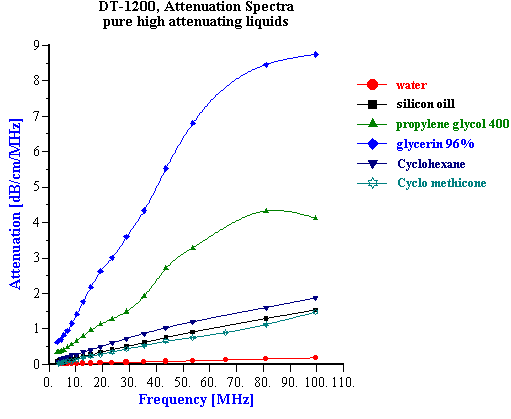
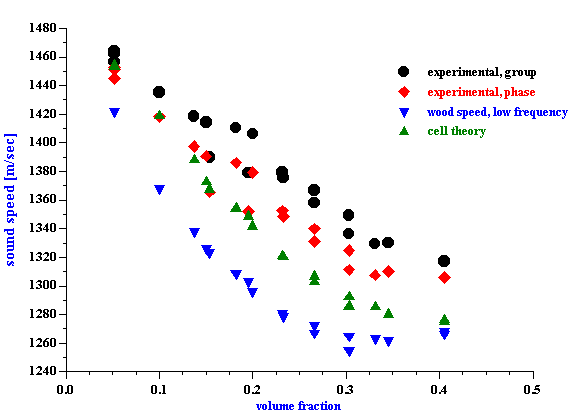
It has been known for quite some time that the acoustic properties of a homogeneous liquid depend on its chemical composition and there have been several successful attempts to use ultrasound for characterizing the chemical properties of such liquids [1-10]. However, for the colloid scientist it would at first seem that the acoustic properties of pure liquids, and any relationship to their chemical composition, are not so important. It is true that the acoustic response of the dispersion medium plays only the minor role of a “background” against which the acoustic response for the colloid is then measured. However, to accurately characterize these colloidal particles it is desirable that this background signal is known and preferably quite small in comparison to the colloid signal. It would also be helpful if the background signal for a given dispersing media was not sensitive to small changes in the chemistry, since this would allow us to use the same value of the background signal for all dispersions made using this particular liquid. In summary, it appears that some information about the acoustic properties of homogeneous liquids, particularly in regard to changes in chemical composition is indeed important for colloid characterization.

There is one more aspect of potential importance. Acoustics allows us to characterize ionic solutions with very high ionic strength exceeding 1M. This solutions can be considered at some extent as a models of the internal parts of the double layer. It means that acoustics opens the possibility to get information about liquid structure inside of the double layer.

When we speak of “acoustic properties” we include measurement of both acoustic attenuation and sound speed. Each measurement contains useful information about the nature of our colloidal system. However, we will show with various examples below that there are distinct advantages to using the attenuation coefficient as opposed to sound speed for characterizing colloidal dispersions. For the vast majority of real dispersions the chemical composition of the media affects the sound speed far more than it effects the attenuation, when judged with respect to the contribution made by the colloidal particles.

Fortunately, the intrinsic attenuation of many pure liquids is quite small compared to the attenuation of typical concentrated dispersions. For example, Figure 1 illustrates the attenuation for several common liquids. The intrinsic attenuation of water at 100 MHz is only 0.2 dB/cm/MHz and it is the one of the most “transparent” liquid for ultrasound. Of the materials tested, only anilene had a lower attenuation than water. The attenuation progressively increased above that for water as we tested methyl-pyrrodione (SP?), heptane, ethanol, toluene, and kerosene, but all of these still had an attenuation much less than 1 db/cm/MHz at 100 MHz. The attenuation of most concentrated colloid is many times higher as one can see from the data shown on Figure 7 for rutile slurries with various volume fractions. There are many other examples of attenuation spectra in DT newsletters.

The intrinsic attenuation of a single phase liquid can be changed in two ways: adding one liquid to another (“liquid mixtures”); or adding a solid which completely dissolves in the original liquid.

There is a large body of literature devoted to the acoustic properties of the liquid mixtures. Most often either sound speed or attenuation is reported, but typically not both. For instance, one can find much useful data on sound speed in the handbook [10], but there are not many works showing both attenuation and sound speed for the same mixture. We present here just one example of a water-ethanol mixture. Figure 2 shows results of automatic titration of water with ethanol. These results were obtained with the modern Acoustic Spectrometer DT-1200 designed by Dispersion Technology

As illustrated in Figure 2, both the attenuation and sound speed varies with the water-to-ethanol ratio. However, the attenuation spectra remains within the instrument precision (0.01 dB/cm/MHz) up to 20 % of ethanol in water. Even the highest attenuation deviation from the water level at 50:50 mixture is still much lower than typical attenuation coming from the colloid particles and illustrated on Figure 7. Figure 2 gives attenuation at 100 MHz . Attenuation at lower frequencies decays as linear with frequency. This means that it would be even smaller comparing to the attenuation of colloidal particles.

At the same time sound speed exhibits measurable changes exceeding instrument precision (0.1 m/sec) even at 0.5% of ethanol. But most important that this changes are comparable with the sound speed changes caused by colloidal particles (see Figure 7). It means that the variation of the sound speed produced by small chemical contamination might be mistakenly attributed to the colloidal particles which would lead to the erroneous conclusions. The danger to make such a mistake is much less if one deals with attenuation instead of the sound speed.

It is interesting that both the attenuation and sound speed exhibit a strong non-linearity in their dependence on chemical composition. Both go through a maximum. The position of the maximum for sound speed is different than that for attenuation. This means that initial addition of ethanol to water does not affect the viscosity of water but does affect its elasticity. The viscosity of water starts to change only when the ethanol content exceeds 20%. The elastic component at this concentration already decays to the ethanol value. It is not clear why all this happens. However, it is obvious that acoustic properties of liquid mixtures contain a lot of information about their structure.

Another example of the liquids with variable chemistry is electrolyte ion solutions. Ultrasound as a tool for studying the properties of electrolyte solutions has a long history going back to the beginning of 20th century. In 1967 Manfred Eigen, Ronald Norrish and George Porter received a Nobel prize for their work on high speed chemical reactions using “relaxation spectroscopy”. This term defines any experimental technique that is based on the time variation of any thermodynamic parameter. Acoustic spectroscopy is just one form of “relaxation spectroscopy”. Another form, dielectric spectroscopy [11], is perhaps more widely known in Colloid Science. Both techniques were used in the middle of the 20th century for investigating the properties of electrolyte solutions, and Manfred Eigen was the leader of this international group of scientists.

It is ironic that today “relaxation spectroscopy” is almost unknown in Colloid Science, and yet it is very close in terms of technique and application. We repeated some experiments originally performed by Eigen and others. We are not giving here any of the theoretical interpretation developed 50 years ago. We suggest that readers who are interested in this technique read the original papers by Eigen and his colleagues [2,3].

Modern instruments, like the Acoustic Spectrometer DT-1200, are much faster and easier to use than the instrumentation that was available in the middle 20th century. All data presented in Figures 1-6 and Table 1 were collected in just a few days. This higher efficiency allowed us to include one more variable, i.e electrolyte concentration.

Table 1. Measured sound speed and intrinsic attenuation of various 1M electrolytes.

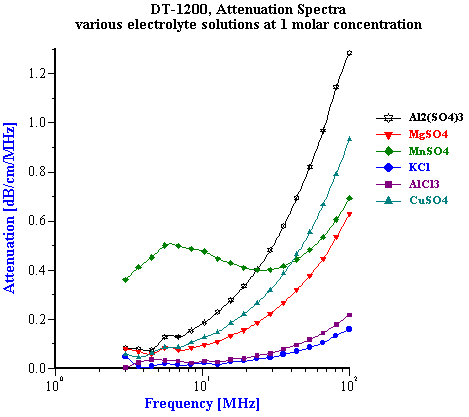
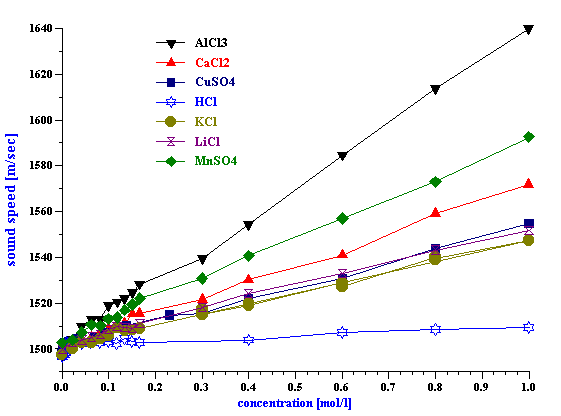
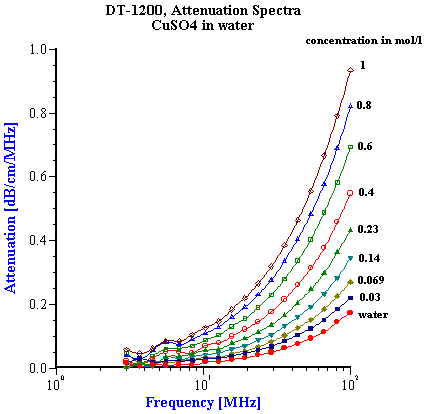
We tested ten different inorganic electrolytes in an effort to compare the results to pure water. As shown in Table 1, none of the four uni-valent electrolytes ( HCl, KCl, LiCl, NaCl) increased the 100 MHz attenuation above that found for pure water. The bi-valent CaCl2 Only five of the selected electrolytes exhibited any effect on the attenuation spectra (see Figure ????).Manganese Sulfate (MnSO₄) produced the most unusual and interesting effect on the attenuation spectra. Figure 6 illustrates attenuation spectra of this electrolyte for various concentrations. These curves repeat results obtained 30 years ago by Jackopin and Yeager [7].

Effects on attenuation spectra observed for MnSO₄ , CuSO₄ , Al₂ (SO₄ )₃ are known as the strongest known according to the paper by Eigen [2]. For our further application of acoustics to colloids, it is important to conclude that for electrolyte concentration below 0.1 M attenuation changes less than 0.1 dB/cm/MHz. Colloidal particles cause much higher effects on the attenuation. It means, that possible variation of intrinsic background attenuation of the dispersion medium due to the ion composition is negligible. It must be taken into account only for very high ion concentrations approaching 1 M level.

Situation with the sound speed is rather different. Table 1 shows sound speed of 1M electrolyte solutions. It is seen that it changes even for 1:1 electrolytes. Magnitude of this change is comparable with contribution of colloidal particles. They are comparable even at low ion concentrations. Figure 4 shows dependence of sound speed on the ion concentration for all 10 electrolytes. It is seen that it is practically linear function of the concentration. This effect can be measured even below 0.1 M taking into account that precision of the sound speed measurement with DT-1200 is about 0.1 m/sec.

It is interesting that the linear dependence of the sound speed – ion concentration cannot be explained with increasing due to the added electrolyte density. According to the general acoustics sound speed c_m depends on density rm and compressiblity b :

It means that sound speed should decay with increasing density if we assume compressibility constant. Experiment indicates just opposite. According to the data given in the Table 1, sound speed increases with increasing density of the electrolyte solution. This density was measured using a liquid pyncnometer.

Increase of the sound speed with density indicates that compressibility is not constant. It is also function of the ions concentration. It follows that compressibility of liquid decays with increasing electrolyte concentration. It looks like ions enforces the structure of the liquid. This effect becomes stronger for higher charged ions, as it is shown in the Table 1.

This effect might be important for understanding the nature of the internal parts of the double layers where electrolyte concentrations becomes very high. Acoustics allows us to characterize the properties of the liquids at such extreme ionic strength. It yields information about both real and imaginary reological components. Attenuation is related to the viscous component, whereas compressibility calculated from the sound speed is close to elasticity. Experiments mentioned above indicate that both real and imaginary components depends on the electrolyte concentration. It means that both elasticity and viscosity of the liquid within the double layer are different than in the bulk of the solution. Concerning viscosity, it is known for a long time [11]. The concept of water elastisity change within the DL is rather new. It is not clear yet what consequencies to the DL theory it might bring.

Bibliography.

P.M.Morse and K. Uno Ingard, Theoretical Acoustics, Princeton University Press, NJ, 1986

Eigen., “Determination of general and specific ionic interactions in solution”, Faraday Soc. Discussions, 1957, No.24, p.25

Eigen and deMaeyer, in “Techniques of Organic Chemistry”, (ed. Weissberger) Vol. VIII Part 2, Wiley 1963, p.895

V.A.Solovyev, C.J.Montrose, M.H.Watkins and T.A.Litovitz, “Ultrasonic Relaxation in Etnanol-Ethyl Halide Mixtures”, J.of Chemical Physics, vol.48, 5, (1968), pp. 2155-2162

G.D’Arrigo, L.Mistura and P. Tartaglia, ” Sound Propagation in the Binary System Aniline-Cyclohaxane in the Critical Region”, Physical review A, vol.1, 2, (1974), pp. 286-295

O.Nomoto and T.Kishimoto, “Velocity and Dispersion of Ultrasonic Waves in Electrolytic Solutions”, Bulletin of Kobayashi Institute, vol.2, 2 (1952) pp. 58-62

Leroy Jackopin and Ernest Yeager, “Ultrasonic Relaxation in Manganese Sulfate Solutions”, J.of Physical Chemistry, vol.74, 21, (1970), pp. 3766-3772

T.A.Litovitz and Lyon, “Ultrasonic Hysteresis in Viscous Liquids”, J.Acoust.Soc.Amer., vol.26, 4, (1954) pp. 577- 580

A.G.Chynoweth and W.G.Scheider, “Ultrasonic Propagation in Binary Liquid Systems near Their Critical Solution Temperature”, J.of Chemical Physics, vol.19, 12 (1951), pp.1566-1569

Numerical data and functional relationships in Science and Technology, Ed. K.H.Hellwege, Vol. 5, Molecular Acoustics, Ed. W.Schaaffs, Berlin, NY, 1967

J.Lyklema, “Fundamentals of Interface and Colloid Science”, vol. 1-3, Academic Press, London-NY, 1995-2000.

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6

Figure 7.

DT-1200, Sound Speed of Rutile R-900