Particle Size Distribution and Micro-Rheological Properties of the Structured Concentrated Dispersions
Andrei S.Dukhin, Philip J.Goetz
Shin-ichi Takeda
Okayama University, Dept. of Applied Chemistry, 3-1-1 Tsushima-naka, Okayama, Japan-700
The biggest advantage of acoustic spectroscopy over other spectroscopic methods is the ability to characterize concentrated dispersed systems without dilution. The frequency dependence of the sound attenuation is the normal experimental output of this measurement. This frequency spectra can then be converted to the particle size distribution.
This conversion procedure requires a theory for sound propagation through the dispersed system. The most complete theory for the concentrated case exists for sub-micron particles with a high density contrast [ 3,4 ]. This theory takes into account hydrodynamic particle-particle interaction, which is important for the viscous component of the sound attenuation. In addition this theory describes contribution of the specific forces which are modeled as flexible strings connecting particles. This second contribution is usually called “structural losses”.
This additional mechanism of the sound attenuation complicates characterization of the particle size distribution. Fortunately, in many cases structural losses are negligible even at very high volume fractions. For instance, experimental dilution test with concentrated rutile [ 3,5 ] and silica [ 5 ] dispersions yields correct particle size taking into account only viscous losses.
However, there are some instances when theory of viscous losses only fails to fit the experimental data. One such examples is given in the paper of several Japanese scientists [ 6 ]. We will use this paper in order to show that the additional mechanism of structural losses provides required theoretical framework for characterizing particle size distribution in the highly concentrated (up to 40%vl) and not completely stable dispersions.
There are six known mechanisms of sound interaction with a dispersed system: 1) viscous; 2) thermal ; 3) scattering; 4) intrinsic; 5) structural; and 6) electrokinetic. In this work we consider only the viscous, intrinsic and structural loss mechanisms. These three mechanisms are sufficient for characterizing the propagation of sound through dispersions of high density contrast rigid particles having a diameter less than 3 microns. The viscous losses of the acoustic energy occur due to the shear wave generated by the particle oscillating in the acoustic pressure field. These shear waves appear because of the difference in the densities of the particles and medium. This density contrast causes a particle motion with respect to the medium. As a result the liquid layers in the particle vicinity slide relative to each other. This sliding non-stationary motion of the liquid near the particle is referred to as “shear wave”.
The intrinsic losses of the acoustic energy occur due to the interaction of the sound wave with the materials of the particles and medium as homogeneous phases.
The oscillation of the network of interparticle links in a structured dispersed system causes structural losses. Thus, this mechanism is specific for structured systems.
The coupled phase theory for the viscous and structural losses is based on balancing the forces on both the particles and the liquid as well as applying the law of conservation of mass. These force balance equations should take into account the “specific” forces [ 7 ] as well as the hydrodynamic forces. Specific forces act like springs connecting particles following the general transient-network theory created in the works [ 7,8 ]. The simplified version of this model allows one to calculate the complex wave number.
Two terms are necessary to present adequately the contribution of the non-Hookean springs to the force balance. First term is a Hook’s force proportional to the displacement of the particle with a coefficient b . The second term is a dissipative force proportional to the particle velocity with a coefficient d . Coefficients b and d are assumed to be the same for the all particles. This assumption is a logical first step in incorporating structural effects in the theory of sound propagation through a polydisperse system.
The resulting expression for the complex wavenumber l has been derived in the work [ 3 ]:
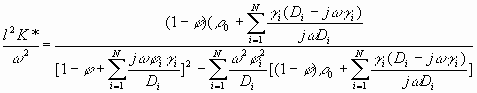
(1)
where
![]()
![]()
where K* is a bulk modulus, the reciprocal of compressibility, w is a frequency of sound, j is the volume fraction of the disperse phase, j is imaginary unit, a is particle radius, h is dynamic viscosity, r o and r p are the density of the media and particle respectively, the index i corresponds to the ith fraction of the particle size distribution, and W is a Stoke’s drag coefficient calculated from the separate hydrodynamic problem described in the paper [ 3 ].
The attenuation of ultrasound a and sound speed V are related to the complex wavenumber with the following expressions:
![]()
(2)
V= w /Re(l) (3)
Expression 1 is more general than the original “coupled phase theory” . First of all, it is valid for a polydisperse system, which is rather important since practical systems might be polydisperse not only in size but also with respect to density or perhaps other physical properties. The more general theory allows us to treat systems with mixed dispersed phases containing particles of the different chemical nature and different internal structure [ 9 ].
In addition, this theory yields an expression for the complex wavenumber in the gels. Attenuation of gels is caused just by oscillation of the polymer network, or in our terminology it is only “structural losses”. By assuming that the drag coefficient g is equal to zero in Equation 1, we have the following expressions for gels:
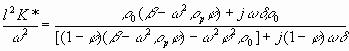 (4)
(4)
This expression can be used for calculating the attenuation and sound speed in pastes and gels. It has not yet been tested experimentally. It is seen that attenuation occurs only when the second virial coefficient is not zero.
Figures 1 and 2 illustrate effect of the structure on the attenuation spectra of 40%vl alumina dispersion with median size 1 micron. It is seen that the first virial coefficient just shifts the critical frequency, keeping the shape of the curve more or less intact and the peak attenuation constant. Since the particle size is reciprocally proportional to the square root of this critical frequency, the influence of the structure must be very substantial in order to create large errors in the particle size.
Influence of the first virial coefficient could not affect quality of fitting. For instance, it cannot explain possible excess attenuation. Elastic structure does not change the amplitude of attenuation. Excess attenuation observed on experiment can be related only with the second virial coefficient, as it follows from the Figure 2.
In principle, this second virial coefficient can be extracted from the attenuation spectra as an adjustable parameter. Next sections illustrate this method.
EXPERIMENT.
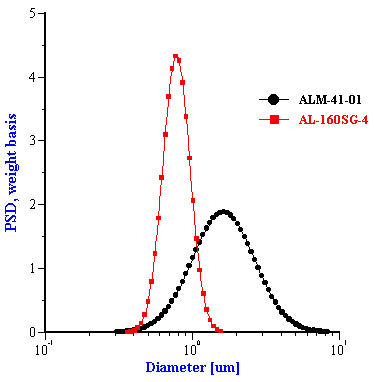
We use experiments performed at the National Institute for Resources and Environment, Tsukuba, Japan [6]. They used two alumina powders: Showa Denko AL-160SG-4 and Sumitomo Chemical Industry ALM-41-01. The median size of the each powder was measured by laser diffraction using a Sympatec Helos and by photo-centrifugation using a Horiba CAPA-700. This data is summarized in Table 1.
Both samples were stabilized with sodium polycalboxyl acid as a surfactant and ball milled for 3 days. The volume fractions of the slurries varied from 1% to 40%.
They used PenKem Acoustophor 8000 for measuring the acoustic attenuation spectra of these slurries. The particle size calculated from these attenuation spectra agreed with independent measurements at volume fractions below 20%. This size data is summarized in Table 1.
The attenuation at the highest volume fraction is shown on Figure 3. We have reproduced these curves from the published graphs because the numerical data was not available in their paper. As a result, one may assume some small deviations from the original data. We use attenuation spectra at the highest volume fraction in the further analysis.
RESULTS and DISCUSSION
Figures 4 shows the experimental and theoretical attenuation spectra at the highest volume fractions, about 40% vl for both alumina samples. It is seen that the theory does not fit the experimental data very well since the experimental attenuation exceeds the theory by a substantial degree. Based on this excess, the authors concluded that there is an unknown factor which becomes significant at high volume fraction.
We suggest “structural losses” as this hypothetical factor. We used Equation 1 for calculating the theoretical attenuation spectra. We assumed that the first virial coefficient b is zero. The second virial coefficient is then used as an adjustable parameter in addition to median size and standard deviation of the lognormal particle size distribution. This searching routine looks for the particle size distribution which generates a theoretical attenuation spectra which fits the experimental spectra with the least error.
The addition of this new adjustable parameter, d , allowed us to achieve much better theoretical fit as illustrated in Figure 5. Table 1 gives the results of the calculated particle sizes and fitting errors. It is seen that the addition of these structural losses leads to dramatic improvements in the fitting error, which strongly suggests that this mechanism can indeed explain the observed excess attenuation.
The particle size data confirms this conclusion as well. It is seen that particle size calculated including these structural losses are much closer to independent measurement performed with diluted system using light based instruments.
It is interesting that the value of the second virial coefficient turns out to be the same for both samples, 0.8. It is independent on the particle size, as it is supposed to be. This parameter characterizes flexibility of reology of the polymer chains linking particles together into the structure at high volume fractions.
We would like to finish with warning, that addition of the structural losses is justified only when traditional theory fails and experiment shows an excess attenuation. This excess attenuation is a source of experimental information for calculating microreolgical properties.
REFERENCES
1.Epstein, P.S. and Carhart R.R., “The Absorption of Sound in Suspensions and Emulsions”, J.of Acoust.Soc.Amer., 25, 3, 553-565 (1953)
2.Allegra, J.R. and Hawley, S.A. “Attenuation of Sound in Suspensions and Emulsions:Theory and Experiments”, J.Acoust.Soc.Amer., 51, 1545-1564 (1972)
3. A.S.Dukhin and P.J.Goetz, “Acoustic Spectroscopy for Concentrated Polydisperse Colloids with High Density Contrast”, Langmuir, 12 [21] 4987-4997, 1996.
4. Dukhin, A.S. and Goetz, J.P. “Acoustic and electroacoustic spectroscopy for characterizing concentrated dispersions and emulsions”, Advances in Colloid Interface Sci., 2000
5. Dukhin, A.S., Shilov, V.N, Ohshima, H., Goetz, P.J “Electroacoustics Phenomena in Concentrated Dispersions. New Theory and CVI Experiment”, Langmuir, 15, 20, 6692-6706, 1999
6. Hayashi, T., Ohya, H., Suzuki, S., Endoh, S., ” Errors in Size Distribution Measurement of Concentrated Alumina Slurry by Ultrasonic Attenuation Spectroscopy”, J.Soc. Powder Techn., Japan, 498-504 (2000)
7. Lyklema, J. “Fundamentals of Interface and Colloid Science”, Volumes 1, Academic Press, 1993
8. Chen, M. And Russel, W.B. “Characteristics of Flocullated Silica Dispersions”, J.Colloid Interface Sci., 141, 2, 564-577 (1991)
9. Dukhin, A.S. and Goetz, J.P. “Characterization of Concentrated Dispersions with Several Dispersed Phases by Means of Acoustic Spectroscopy”, accepted, Langmuir (2000)
Table 1. Particle size of the two alumina samples
|
Median particle size [micron] |
||
|---|---|---|
|
ALM-41-01 |
AL-160SG-4 |
|
|
Size, Horiba |
1.47 |
0.56 |
|
Size, Sympatec |
1.98 |
0.71 |
|
Size, PenKem, vfr<20% |
1.79 |
0.52 |
|
Size, Acoustics, vfr=40% with structural losses |
1.63 (fit error 6.1%) |
0.77 (fit error 2.3%) |
|
Size, Acoustics, vfr=40% no structural losses |
1.07 (fit error 19.2%) |
0.8 (fit error 18.4%) |
Figure 1.
Theoretical attenuation of the 40%vl alumina slurry with 1 micron particles at different values of the first virial coefficient assuming the second virial coefficient to be a zero.
Figure 2.
Theoretical attenuation of the 40%vl alumina slurry with 1 micron particles at different values of the second virial coefficient assuming the first virial coefficient to be a zero.
Figure 3.
Experimental attenuation spectra of the two alumina slurries characterized in the paper [6].
Figure 4
Theoretical fit to the experimental data presented in the paper [6] assuming no structural losses.
Figure 5.
Theoretical fit to the experimental data presented in the paper [6] with structural losses.
Figure 6
Particle size distribution calculated for the two alumina samples described in the paper [6].
Figure 1
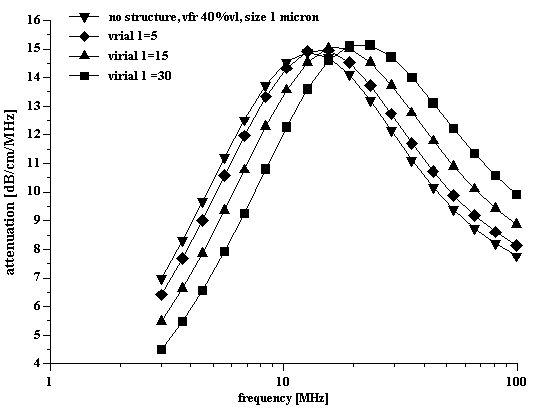
Figure 2
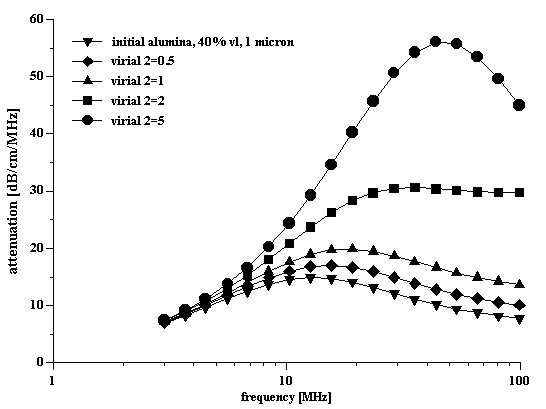
Figure 3
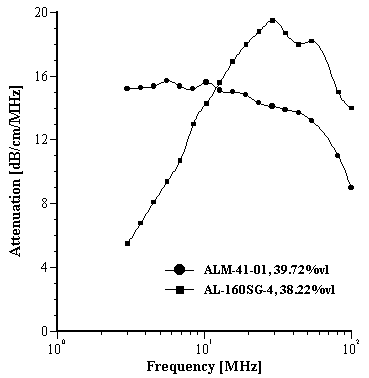
Figure 4

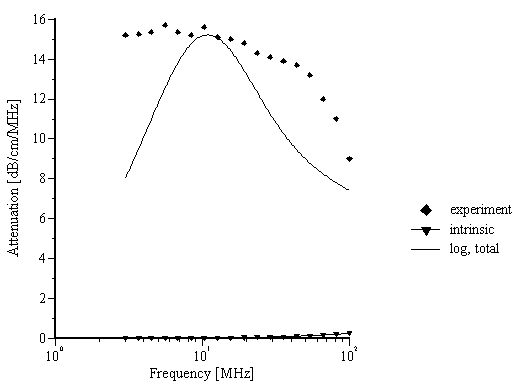
Figure 5

Figure 6