Particle Size – A Short Tutorial
INTRODUCTION
Particle size is a geometric characteristic that is usually assigned to material objects with sizes ranging from nanometers to millimeters. There is a wide variety of real systems that contain particles within this size range. These systems are generally polydisperse. Therefore, the particles in a particular sample vary in size. It is not sufficient to simply determine a single particle size in order to adequately characterize such systems. Instead, we must instead determine the system’s particle size distribution.
Measurements of the particle size and particle size distribution are extremely important tools for research and development, as well as a quality control, in many industries. These industries include pharmaceuticals, cements, ceramics, paints, emulsions, etc. There are three distinctively different groups of the particle sizers: 1) counters; 2) fractionation methods; 3) macroscopic fitting methods. Below we present links to several International Standards which provide descriptions of some of these methods.
MACROSCOPIC FITTING TECHNIQUES.
Methods that are classified as macroscopic fitting techniques include light scattering, x-ray scattering, neutron scattering, and acoustic spectroscopy. All of these methods rely on the measurement of a certain property of a sample that contains particles. The particle size distribution is extracted then from this measured raw data using an appropriate theory. In the case of static light scattering instruments, the raw data measured is the intensity of scattered light versus angle. Calculation of the particle size distribution requires a theory. It relates this information to particle size. Theoretical aspects of the light scattering are well known and described in detail in the ISO standards referenced below.
ACOUSTIC SPECTROSCOPY.
Acoustic spectroscopy belongs to the group of macroscopic fitting methods as well. However, it stands alone from other macroscopic methods because of its capability of characterizing concentrated systems without dilution. This method is based on measuring the attenuation of ultrasound at a set of frequencies in the MHz range when propagation distance varies. Accordingly, such attenuation spectrum is the raw data for calculating particle size distribution. There is a well-developed theory that takes into account particles’ interactions, which is imperative when extracting particle size distributions from attenuation spectra in concentrated systems. Details of this method are described in the International Standard ISO 20998-1:2006 “Measurement and characterization of particles by acoustic methods — Part 1: Concepts and procedures in ultrasonic attenuation spectroscopy”.
Many different groups verified the theory for the acoustic spectroscopy using a wide variety of samples. Some results of such verification are presented in the book “Characterization of Liquids, Nano- and Microparticulates, and Porous Bodies using Ultrasound” (2017). Consequently, the verification tests confirm that this method yields particle size distributions that are very close to those determined using other characterization techniques.
VERIFICATION TEST
Here we present the results of such a verification test when comparing DLS, Centrifugation, ELS, X-ray scattering, and acoustic spectroscopy. Silica Koestrsol served as a sample for all measurements. This silica serves as a basis for an EU certified reference material. Details of these experimental tests are described in ref.4.
| Method | Particle size value [nm]. |
|---|---|
| Dynamic light scattering, intensity massed harmonic mean diameter by cumulants method. | 19.0 ± 0.6 |
| Centrifuge liquid sedimentation, intensity based modal diameter. | 20.1 ± 1.3 |
| Electron microscopy, number based mean diameter. | 19.4 ± 1.3 |
| Small X-rays scattering, number based mean diameter. | 21.8 ± 0.7 |
| Acoustics, mass based median diameter. | 22.4 ± 0.5 |
Acoustic spectroscopy makes it possible to perform particle size measurements when no dilution and no sample preparation involved. This is critical in many cases when dilution affects particle size distribution. Furthermore, this method is suitable for characterizing structured dispersions as well. Such structure when it formed by polymer network contributes to ultrasound attenuation by itself. But this contribution can be subtracted using appropriate existing theory. In addition, acoustic spectroscopy can resolve particle size distributions of different species of particles in mixed dispersions, if they have different densities.
This method can also monitor particle size during milling, crystallization, and other industrial processes. One of the most important applications of acoustic spectroscopy is determining particle size of nano-dispersions and other nano-particulates. Acoustics can monitor the presence of nanoparticles with a precision of 1%, whereas nanoparticles can be masked by larger particles when other methods are used.
PARTICLE SIZE DISTRIBUTION.
In order to characterize the polydispersity of real dispersions and emulsions we use the well-known concept of the “particle size distribution” (PSD). A detailed description of this concept can be found in the publications of Leschonski [5]. There are multiple ways to represent PSD depending on the principles of the measurement and particles’ properties. Generally, the independent variable (abscissa) describes the physical property chosen to characterize the size. Meanwhile, the dependent variable (ordinate) characterizes the type and measure of the quantity. It does it either on number, or area, or volume, or weight.
Assumption of a unique relationship between the physical property and a one-dimensional property unequivocally defining “size” underlines this approach. This assumption is only approximate. Markedly, for irregular particles, the concept of an “equivalent diameter” allows one to characterize such entities using a single parameter. This parameter is the diameter of a sphere that yields the same value of any given physical property when analyzed under the same conditions as the irregularly shaped particle.
The different relative number of particles, measured in certain size intervals, form a so-called density distribution that represents the first derivative of the cumulative distribution. The cumulative distribution is usually normalized. This distribution determines the number of particles (in number, length, area, weight or volume depending on r) that are smaller than the equivalent diameter X.
HISTOGRAM
The figure below shows the normalized discrete density distribution or histogram qr(Xi,Xi+1). This distribution specifies the number of particles having diameters larger than xi and smaller than xi+1 :
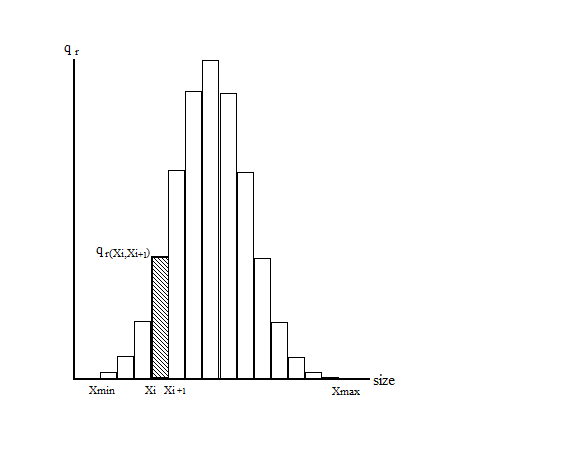
The shaded area represents the relative amount of the particles. The histogram transforms to a continuous density distribution when the thickness of the histogram column limits to zero. Histogram reflects PSD adequately when we know the value of each particle size fraction. It is the so-called “full particle size distribution”. Counting and fractionation techniques can measure it. However, in many cases, full information about the PSD is either not available or not even required. Therefore, various analytical particle size distributions replace histograms.
There are several analytical particle size distributions that approximately describe empirically determined particle size distributions. One of the most useful is the log-normal distribution. Log-normal distributions require that we extract only two parameters from the experimental data – median size and standard deviation. Consequently, this is a big advantage in many cases with limited amount of the experimental data.
INTERNATIONAL STANDARDS FOR PARTICLE SIZING
22412:2008 “Particle size analysis — Dynamic light scattering (DLS)”
13320:2009 “Particle size analysis — Laser diffraction methods”
REFERENCES.
- Wikipedia Article on “Particle_size”
- Wikipedia Article on “Particle Size Distribution”
- Dukhin, A.S. and Goetz, J.P. “Characterization of Liquids, Nano- and Microparticulates, and Porous Bodies using Ultrasound”, Edition 3, Elsevier, 571 pages, 765 references, (2017).
- Dukhin, A.S., Parlia, S., Klank, D., Lesti, M. “Particle sizing and zeta potential of silica Koestrol (basis for certified reference material ERM-FD100 for Nanoparticles) by Acoustics and Electro-acoustics”,Part.Part.Syst.Charact.,27,pp.165-171, (2010).
- Leschonski, K. “Representation and Evaluation of Particle Size Analysis data”, Part. Charact., 1, 89-95 (1984)
