Model Theory
model theory…
First, any model for the dispersed phase particles must describe the properties of a single particle: its shape, physical and chemical properties, etc. The model must also reflect any possible polydispersity, i.e. the variation in properties from one particle to another. This is a rather difficult task. Fortunately, at least with particle shape, there is one factor that helps – Brownian motion.
Colloidal particles are generally irregular in shape. There are of course a small number of exceptions such as emulsions or latices. All colloidal particles experience Brownian motion that constantly changes their position. A natural averaging occurs over time; the resulting time averaged particle looks like a sphere with a certain “equivalent diameter”, d. It is for this reason that a sphere is the most widely and successfully used model for particle shape.
Obviously a spherical model does not work well for very asymmetric particles. Here an ellipsoid model can yield more useful results [10-12]. This adds another geometrical property: an aspect ratio, the ratio of the longest dimension to the shortest dimension. For such asymmetric particles the orientation also becomes important, bringing yet further complexity to the problem.
Here we will simply assume that the particles can be adequately represented by spheres. This assumption affects ultrasound absorption much more than ultrasound scattering, as is the case with light scattering. According to both our experience and preliminary calculations for ultrasound absorption [12] this spherical assumption is valid for aspect ratios less than 5:1.
The material of the dispersed phase particles is characterized with the same set of gravimetrical, rheological, thermodynamic, electrodynamic, acoustic and electroacoustic parameters as the material of the dispersion medium described in the Chapter 1 of the [105]. We will use the same symbols for these parameters, changing only the subscript index to p.
The fact that we define so many properties for both the media and the particles does not mean that, in order to derive useful information from the measured acoustic or electroacoustic measurement, we need to know this complete set for a particular dispersion. Chapter 4 of the book [105] outlines the set of input properties that are necessary to constructively use ultrasound measuring techniques. The exact composition of this required set depends on the nature of the particles, particularly on their rheology. In this regard, it turns out that it is very useful to divide all particles into just two classes, namely rigid and soft.
Rigid vs. soft particles
Historically, Morse and Ingard [5] introduced these two classes of rigid and non-rigid (soft) particles to the acoustic theory for describing ultrasound scattering. In the case of scattering, the notion of a rigid particle serves as an extreme but not real case. It turns out that this classification is even more important in the case of ultrasound absorption.
In the case of ultrasound absorption, the notion of rigid particles corresponds to real colloids, such as all kinds of minerals, oxides, inorganic and organic pigments; indeed, virtually everything except for emulsions, latices and biological material. Rigid particles dissipate (absorb) ultrasound without changing their shape in either an applied sound field or an electric field. For interpreting ultrasound absorption caused by rigid particles, we need to know, primarily, the density of the material. There is no need to know any other gravimetric or acoustic properties or, in fact, any rheological, thermodynamic, electrodynamic or electroacoustic properties at all. Furthermore, the sound speed of these rigid particles is, usually, close to 6000 m/sec. Thus, in most cases, we can simply assume that this same value is appropriate. The sound attenuation inside the body of these particles is usually negligible. We do not need to know the electrodynamic properties, except in rare cases of conducting and semi-conducting particles.
It is important to mention here that sub-micron metal particles are not truly conducting. There is not enough difference in electric potential between particle poles to conduct an electrochemical reaction across the small distance between these poles. Such sub-micron particles represent a special case of so-called “ideally-polarized particles” [33].
These empirical observations reduce the number of parameters, required to characterize rigid particles, to just one, namely the density. It is also important to mention that most often the density of these particles significantly exceeds that of the liquid media.
The situation with soft particles is very different. First, the density of these softer particles quite often closely matches the density of the dispersion media. As a result, all effects, which depend on the density contrast are minimized. Instead, thermodynamic effects are much more important and the thermal expansion coefficient of the particle and suspending media replace the density contrast as a critical parameter for ultrasound absorption.
So far we have talked about particles that are internally homogeneous, constructed from the same material. However, there are some particles that are heterogeneous inside, consisting of different materials at different points within their bodies. Usually a “shell model” is used to describe the properties of these complex particles [13, 16]. Occasionally a simple averaging of properties over the particle volume suffices, as for instance, using an average density.
Particle size.
Colloidal systems are generally of a polydisperse nature – i.e. the particles in a particular sample vary in size. Aggregation, for instance, usually leads to the formation of polydisperse sols, mainly because the formation of new nuclei and the growth of established nuclei occur simultaneously, and so the particles finally formed are grown from nuclei formed at different times.
Table 1. Representation of PSD Data
| Measure of quantity
Type of quantity |
Cumulative Qr | Density |
| r=0 : number | Cumulative PSD on number basis | Density PSD on number basis |
| r=1 : length | Figure 2.5. | Figure 2.4 |
| r=2 : area | Cumulative PSD on area basis | Density PSD on area basis |
| r=3 : volume, weight | Cumulative PSD on weight basis | Density PSD on weight basis |
In order to characterize this polydispersity we use the well-known conception of the “particle size distribution” (PSD). We define this here following Leschonski [14] and Irani [15].
There are multiple ways to represent the PSD depending on the physical principles and properties used to determine the particle size. A convenient general scheme created by Leschonski is reproduced in Table 1.
The independent variable (abscissa) describes the physical property chosen to characterize the size, whereas the dependent variable (ordinate) characterizes the type and measure of the quantity. The different relative amount of particles, measured in certain size intervals, form a so-called density distribution, qr(X) that represents the first derivative of the cumulative distribution, Qr (X). The subscript, r, indicates the type of the quantity chosen.
Figure 2 and 3 illustrate the density and cumulative particle size distributions. The parameter, X, characterizes a physical property uniquely related to the particle size. It is assumed that a unique relationship exists between the physical property and a one-dimensional property unequivocally defining “size”.
This can be achieved only approximately. For irregular particles, the concept of an “equivalent diameter” allows one to characterize irregular particles. This is the diameter of a sphere that yields the same value of any given physical property when analyzed under the same conditions as the irregularly shaped particle.
The cumulative distribution, Qr (X) on Figure 3 is normalized. This distribution determines the amount of particles (in number, length, area, weight or volume depending on r) that are smaller than the equivalent diameter X.
Figure 4 shows the normalized discrete density distribution or histogram qr(Xi,Xi+1). This distribution specifies the amount of particles having diameters larger than xi and smaller than xi+1 and is given by:
(1)
The shaded area represents the relative amount of the particles.
The histogram transforms to a continuous density distribution when the thickness of the histogram column limits to zero. It is presented in Figure 2.7 and can be expressed as the first derivative from the cumulative distribution:
(2)
A histogram is suitable for presentation of the PSD when the value of each particle size fraction is known. It is the so-called “full particle size distribution”. It can be measured using either counting or fractionation techniques. However, in many cases, full information about the PSD is either not available or not even required. For instance, Figure 5 represents histograms with a non-monotonic and non-smooth variation of the column size. This might be related to fluctuations and have nothing to do with the statistically representative PSD for this sample. That is why in many cases histograms are replaced with various analytical particle size distributions.
There are several analytical particle size distributions that approximately describe empirically determined particle size distributions. One of the most useful, and widely used distributions, is the log-normal. In general, it can be assumed that the size, X, of a particle grows, or diminishes, according to the relation [15]:
This equation reflects the obvious fact that when d approaches either Xmax,,,, or Xmin, it becomes independent of time. Using assumptions of the normal distribution of growth and destruction times, combined with Equation 3, leads to:
whereand s l are two unknown constants that can have some certain physical meaning, especially for the standard log-normal PSD (Equation 5). The distribution given with Equation 4 is called the “modified log-normal”. It is not symmetrical on a logarithmic scale of particle sizes. One example of a modified log-normal PSD is shown in Figure 5.
Figure 5. Transition from the discrete to the contineous distribution.
For the case when Xmin = 0 and Xmax x x x x = infinity, the modified log-normal PSD reduces to the standard log-normal PSD:
Parameters and s l are then the geometrical median size and geometrical standard deviation. The median size corresponds to the 50% point on the cumulative curve. The standard deviation characterizes the width of the distribution. It is smallest (s l =1) for a monodisperse PSD. It can be defined as the ratio of size at 15.87% cumulative probability to that at 50%, or the ratio at 50% probability to that at 84.13%. These points, at 16% and 84% roughly, are usually reported together with the median size at 50%.
Log-normal and modified log-normal distributions require that we extract only a few parameters (2 and 4 respectively) from the experimental data. This is a big advantage in many cases when amount of the experimental data is restricted. These two distributions plus a bimodal PSD as the combination of two lognormals are usually sufficient for characterizing the essential features of the vast majority of practical dispersions.
Zeta potential and parameters of the model interfacial layer.
In the previous two sections we have introduced a set of properties to characterize both the dispersion medium and the dispersed particles. It is clear that the same properties might have quite different values in the particle as compared to the medium. For example, in an oil-in-water emulsion, the viscosity and density inside the oil droplet would be quite different than the values in the bulk of the water medium. However, this does not mean that these parameters change stepwise at the water-oil interface. There is a certain transition, or interfacial layer, where the properties vary smoothly from one phase to the other. Unfortunately, there is no thermodynamic means to decide where one phase or the other begins. A convention suggested by Gibbs resolves this issue [1], but the details of this rather complicated thermodynamic problem are beyond the scope of this book.
We wish to discuss here only the electrochemical aspects of this interfacial layer and these are generally combined as the concept of the “electric double layer” (DL). Lyklema [1] made a most comprehensive review of this concept, which plays such an important role in practically all aspects of Colloid Science. We present here a short overview of the most essential features of the DL, with particular emphasis on those that can be characterized using ultrasound based technology.
We will consider the DL in two states: equilibrium and polarized. We use term “equilibrium” as a substitute for the term “relaxed” used by Lyklema [1] (The term relaxed is somewhat more general, and might include situations when the DL is created with non-equilibrium factors. For instance, the DL of living biological cells might have a component that is related to the non-equilibrium transmembrane potential [16, 17]. )
For the first equilibrium state, the DL exists in an undisturbed dispersion characterized by a minimum value of the free energy. The second “polarized” state reflects a deviation from this equilibrium state due to some external disturbance such as an electric field.
Figure 6. Illustration of the structure of the electric double layer.
According to Lyklema: “…the reason for the formation of a “relaxed” (“equilibrium”) double layer is the non-electric affinity of charge-determining ions for a surface…”. This process leads to the build up of an “electric surface charge”, s , expressed usually in m C cm-2. This surface charge creates an electrostatic field that then affects the ions in the bulk of the liquid ( Figure 6). This electrostatic field, in combination with the thermal motion of the ions, creates a countercharge, and thus screens the electric surface charge. The net electric charge in this screening diffuse layer is equal in magnitude to the net surface charge, but has the opposite polarity. As a result the complete structure is electrically neutral. Some of the counter-ions might specifically adsorb near the surface and build an inner sub-layer, or so-called Stern layer. The outer part of the screening layer is usually called the “diffuse layer”.
What about the difference between the surface charge ions and the ions adsorbed in the Stern layer? Why should we distinguish them? There is a thermodynamic justification [1] but we think a more comprehensive reason is kinetic (ability to move). The surface charge ions are assumed to be fixed to the surface (immobile); they cannot move in response to any external disturbance. In contrast, the Stern ions, in principle, retain some degree of freedom, almost as high as ions of the diffuse layer [22, 24, 25, 26, 27].
We give below some useful relationships of the DL theory from Lyklema’s review [1].
The DL thickness is characterized by the so-called Debye length k -1 defined by:
(6)
where the valences have sign included, for a symmetrical electrolyte z+ = -z- = z
For a flat surface and a symmetrical electrolyte, of concentration Cs , there is a straightforward relationship between the electric charge in the diffuse layer, s d , and the Stern potential, y d , namely:
(7)
If the diffuse layer extends right to the surface, Equation 2.13 can then be used to relate the surface charge to the surface potential.
Sometimes it is helpful to use the concept of a differential DL capacitance. For a flat surface and a symmetrical electrolyte this capacitance is given by:
(8)
For a symmetrical electrolyte, the electric potential, y , at the distance, x , from the flat surface into the DL, is given by:
(9)
The relationship between the electric charge and the potential over the diffuse layer is given by:
(10)
where n ± is the number of cations and anions produced by dissociation of a single electrolyte molecule, and is a dimensionless potential given by:
(11)
In the general case of an electrolyte mixture there is no analytical solution. However, some convenient approximations have been suggested [1, 22, 50, 68].
Spherical DL, isolated and overlapped
There is only one geometric parameter in the case of a flat DL, namely the Debye length 1/k . In the case of a spherical DL, there is an additional geometric parameter, namely the radius of the particle, a. The ratio of these two parameters(k a) is a dimensionless parameter that plays an important role in Colloid Science. Depending on the value of k a, two asymptotic models of the DL exist.
A “thin DL” model corresponds to colloids in which the DL is much thinner than particle radius, or simply:
k a>>1 (12)
The vast majority of aqueous dispersions satisfy this condition, except for very small particles in low ionic strength media. If we assume an ionic strength greater than 10-3 mol/l, corresponding to the majority of most natural aqueous systems, the condition k a>>1 is satisfied for virtually all particles having a size above 100 nm.
The opposite case of a “thick DL” corresponds to systems where the DL is much larger than the particle radius, or simply:
k a<<1 (13)
The vast majority of dispersions in hydrocarbon media, having inherently very low ionic strength, satisfy this condition.
These two asymptotic cases allow one to picture, at least approximately, the DL structure around spherical particles. A general analytical solution exists only for low potential:
(14)
This so-called Debye-Hückel approximation yields the following expression for the electric potential in the spherical DL, y(r) , at a distance, r , from the particle center:
(15)
The relationship between diffuse charge and the Stern potential is then:
(16)
This Debye-Hückel approximation is valid for any value of k a, but this is somewhat misleading, since it covers only isolated double layers. The approximation does not take into account the obvious probability of an overlap of double layers as in a concentrated suspension, i.e. high volume fraction. A simple estimate of this critical volume fraction, j over , is that volume fraction for which the Debye length is equal to the shortest distance between the particles. Thus::
(17)
This dependence is illustrated in Figure 7.
Figure 7. Estimate of the volume fraction of the overlap of the electric double layer
It is clear that for k a >> 10 (thin DL) we can consider the DL’s as isolated entities even up to volume fractions of 0.4. However, the model for an isolated DL becomes somewhat meaningless for small k a (thick DL) because DL overlap then occurs even in very dilute suspensions. Theoretical treatments have been suggested for these two extreme cases of DL thickness. Briefly they are:
Thin DL (k a > 10) Loeb-Dukhin-Overbeek [18, 19, 20] proposed a theory to describe the DL structure for a symmetrical electrolyte, applying a series expansion in terms of powers of (k a)-1 . The final result is:
(18)
Thick DL (k a<1). No theory for an isolated DL is necessary, since DL overlap must be considered even in the dilute case. A theory that does include DL overlap has been proposed only very recently [21]:
(19)
where
The constant, A , is obtained by matching the asymptotic expansions of the long distance potential distribution with the short distance distribution; b is the radius of the cell.
This new theory suggests, at last, a way to develop a general approach to the various colloidal-chemical effects in non- aqueous dispersions.
Electric Double Layer at high ionic strength
According to classical theory, the DL should essentially collapse and cease to exist when the ionic strength approaches 1 M. At this high electrolyte concentration, the Debye length becomes comparable with the size of the ions, implying that the counter ions should collapse onto the particle surface. However, there are indications [95-102] that, at least in the case of hydrophilic surfaces, the DL still exists even at ionic strengths exceeding 1 M.
The DL, at high ionic strength, is strongly controlled by the hydrophilic properties of the solid surfaces. The affinity of the particle surface for water creates a structured surface water layer, and this structure changes the properties of the water considerably from that in the bulk.
Figure 8 illustrates the DL structure near a hydrophilic surface. Note the difference between the much lower dielectric permittivity within the structured surface layer, εsur , compared to that of the bulk liquid , εm. There are two effects caused by this variation of the dielectric permittivity [100]
The structured surface layer becomes insolvent, at least partially, to ions.
The structured surface layer may gain electric charge due to the difference in the standard chemical potentials of the ions.
Both effects influence the electrokinetic behavior of the colloids at high ionic strength. The first effect is the more important because it leads to a separation of electric charges in the vicinity of the particle. The insolvent structured layer repels the screening electric charge from the surface to the bulk, and makes Electrokinetics possible, at high ionic strength, if the structured layer retains a certain hydrodynamic mobility in the lateral direction.
A theory of Electroosmosis for the insolvent and hydrodynamically mobile DL at high ionic strength has been proposed by Dukhin and Shilov in a paper which is not available in English. There is a description and reference to this theory in an experimental paper that is available in English [101]. We discuss these effects in more detail in Chapter 5 of [105].
Figure 8. Electric Double Layer near hydrophilic surface with structured water layer.
Polarized state of the Electric Double Layer
External fields may affect the DL structure. These fields might be of various origins: electric, hydrodynamic, gravity, concentration gradient, acoustic, etc. Any of these fields might disturb the DL from its equilibrium state to some “polarized” condition. [1,22].
Such external fields affect the DL by moving the excess ions inside it. This ion motion can be considered as an additional electric surface current, Is ( Figure 9). This current is proportional to the surface area of the particle, and to a parameter called the surface conductivity Ks [1]. This parameter reflects the excess conductivity of the DL due to excess ions attracted there by the surface charge.
The surface current adds to the total current. But there is another component that depends on the nature of the particle, which has the opposite effect. For example, a non-conducting particle reduces the total current going through the conducting medium, simply because the current can not pass through the non-conducting volume of the particle. In the important case of charged non-conducting particles these two opposing effects influence the total current value. The surface current increases the total current, whereas the non-conducting character reduces it. The amplitude of the surface current is proportional to the surface conductivity Ks . The amplitude current arising from the non-conductive character depends on the conductivity of the liquid, Km ; the higher the value the more current is lost, because the conducting liquid is replaced with non-conducting particles.
Figure 9. Mechanism of polarization of the electric double layer
The balance of these two effects depends on the dimensionless number, Du, given by:
(20)
The particle size, a, is in the denominator of Equation 2.26 because the surface current is proportional to the surface of the particle (a2), whereas the reduction of the total current due to the non-conducting particles is proportional to the volume of the particles (a3).
The abbreviation, Du, for this dimensionless parameter was introduced by J. Lyklema. He called it the “Dukhin number” [1] after S. S. Dukhin, who explicitly used this number in his analysis of electrokinetic phenomena [22,33].
The surface electric current redistributes the electric charges in the DL. One example is shown in Figure 9. It is seen that this current produces an excess of positive charge at the right pole of the particle and a deficit at the left pole. Altogether, this means that the particle gains an “induced dipole moment” (IDM) [22, 33] due to this polarization in the external field. A calculation of the IDM value for the general case is a rather complex problem. It can be substantially simplified in the case of the thin DL (k a>10).
There is a possibility to split the total electric field around the particle into two components: a “near field” component and a “far field” component. The “near field” is located inside of the DL. It maintains each normal section of the DL in a local equilibrium. This field is shown as a small arrow inside of the DL in Figure 9.
The “far field” is located outside of the DL, in the electro-neutral area. It is simply the field generated by the IDM.
Let us assume now that the driving external field is an electric field. The polarization of the DL affects all of the other fields around the particles: hydrodynamic, electrolyte concentration, etc. However, all other fields are secondary in relationship to the driving electric field applied to the dispersion. The IDM value, pidm , is proportional to the value of the driving force, the electric field strength, E, in this case. In a static electric field these two parameters are related with the following equation:
(21)
where g ind is the polarizability of the particle.
The IDM value depends not only on the electric field distribution, but also on the distribution of the other fields generated near the particle. For example, the concentration of electrolyte shifts from its equilibrium value in the bulk of the solution, Cs.This effect, called concentration polarization, complicates the theory of electrophoresis, and is the main reason for the gigantic values found for dielectric dispersion in a low frequency electric field.
Fortunately, this concentration polarization effect is not important for ultrasound, since it appears only in the low frequency range where the frequency, w , is smaller than the characteristic concentration polarization frequency, w cp:
(22)
where Deff is the effective diffusion coefficient of electrolyte.
Typically, this concentration polarization frequency is below 1 MHz, even for particles as small as ten nanometers.
The IDM value becomes a complex number in an alternating electric field, as well as polarizability. According to the
Maxwell-Wagner-O’Konski theory [28-30], the IDM value for a spherical non-conducting particle is:
(23)
where the complex conductivity of the media is defined by Equation 2.4 in [105].
The complex conductivity of the charged non-conducting particle is given by:
(23)
The influence of the DL polarization on the IDM decreases as a function of the frequency (following from Equation 23). There is a certain frequency above which the DL influence becomes negligible because the field changes faster than the DL can react. This is the so-called Maxwell-Wagner frequency, w MW , which is defined as:
(24)
So far we have described the polarization of the DL mostly as it relates to an external electric field. Indeed, most theoretical efforts over last 150 years have been expended in this area. However, we have already mentioned that other fields can also polarize the DL. The major interest is to describe in some detail the polarization caused, not by this electric field, but a hydrodynamic field, since this gives rise to the electroacoustic phenomena in which we are interested, see [105].
REFERENCES.
- Lyklema, J. “Fundamentals of Interface and Colloid Science”, Volumes 1, Academic Press, (1993)
- Shilov, V.N., Zharkih, N.I. and Borkovskaya, Yu.B. “Theory of Nonequilibrium Electrosurface Phenomena in Concentrated Disperse System.1.Application of Nonequilibrium Thermodynamics to Cell Model.”, Colloid J., 43,3, 434-438 (1981)
- Handbook of Chemistry and Physics, Ed. R.Weast, 70th addition CRC Press, Florida, (1989)
- Temkin S. “Elements of Acoustics”, 1st sd., John Wiley & Sons, NY (1981)
- Morse, P.M. and Uno Ingard, K., “Theoretical Acoustics”, 1968 McGraw-Hill, NY, 1968, Princeton University Press, NJ, 925 p. (1986)
- Litovitz T.A. and Lyon, “Ultrasonic Hysteresis in Viscous Liquids”, J. Acoust. Soc. Amer., vol.26, 4, pp. 577- 580, (1954)
- Stokes, “On a difficulty in the Theory of Sound”, Phil. Mag., Nov. (1848)
- Cannon D.W. “New developments in electroacoustic method and instrumentation”, in S. B. Malghan (Ed.) Electroacoustics for Characterization of Particulates and Suspensions, NIST, 40-66 (1993)
- Hunter, R.J. “Review. Recent developments in the electroacoustic characterization of colloidal suspensions and emulsions”, Colloids and Surfaces, 141, 37-65 (1998)
- Treffers, R. and Cohen, M., “High resolution spectra of cool stars in the 10- and 20-micron region”, Astrophys. J., 188, 545-552 (1974)
- Fuchs, R., “Theory of the optical properties of ionic crystal cubes”, Phys. Rev., B11, 1732-1740 (1975)
- Pendse, H.P., Bliss T.C. and Wei Han “Particle Shape Effects and Active Ultrasound Spectroscopy”, Ultrasonic and Dielectric Characterization Techniques for Suspended Particulates, Edited by V.A. Hackley and J. Texter, American Ceramic Society, Westerville, OH, (1998)
- Zinin, P.V. “Theoretical Analysis of Sound Attenuation Mechanisms in Blood and Erythrocyte Suspensions”, Ultrasonics, 30, 26-32, (1992)
- Leschonski, K. “Representation and Evaluation of Particle Size Analysis data”, Part. Charact., 1, 89-95 (1984)
- Irani, R.R. and Callis, C.F., “Particle Size: Measurement, Interpretation and Application”, John Wiley & Sons, NY-London, (1971)
- Dukhin, A. S. “Biospecifical Mechanism of Double Layer Formation in Living Biological Cells and Peculiarities of Cell Electrophoresis”. Colloids and Surfaces, 73, 29-48, (1993)
- Karamushka, V.I., Ulberg, Z.R., Gruzina, T.G. and Dukhin, A.S. “ATP-Dependent gold accumulation by living Chlorella Cells”, Acta Biotechnologica, 11, 3, 197-203 (1991)
- Loeb, A.L., Overbeek, J.Th.G. and Wiersema, P.H. “The Electrical Double Layer around a Spherical Colloid Particle”, MIT Press (1961)
- Overbeek, J.Th.G., Verhiekx, G.J., de Bruyn, P.L and Lakkerkerker, J. Colloid Interface Sci., 119, 422 (1987)
- Dukhin, S.S., Semenikhin, N.M., Shapinskaya, L.M. transl. Dokl. Phys. Chem., 193, 540 (1970)
- Zholkovskij, E., Dukhin, S.S., Mischuk, N.A., Masliyah, J.H., Charnecki, J., “Poisson-Bolzmann Equation for Spherical Cell Model: Approximate Analytical Solution and Applications”, Colloids and Surfaces, accepted
- Dukhin S.S. and Derjaguin B.V. “Electrokinetic Phenomena”, Surface and Colloid Science, Ed. E. Matijevic, John Willey & Sons, NY, (1974)
- Hidalgo-Alvarez, R., Moleon, J.A., de las Nieves, F.J. and Bijsterbosch, B.H., “effect of Anomalous Surface Conductance on z -potential Determination of Positively Charged Polystyrene Microspheres”, J.Colloid and Interface Sci., 149, 1, 23-27 (1991)
- Kijlstra, J., van Leeuwen, H.P. and Lyklema, J. “Effects of Surface Conduction on the Electrokinetic Properties of Colloid”, Chem. Soc., Faraday Trans., 88, 23, 3441-3449 (1992)
- Kijlstra, J., van Leeuwen, H.P. and Lyklema, J. “Low-Frequency Dielectric Relaxation of Hematite and Silica Sols”, Langmuir, (1993)
- Myers, D.F. and Saville, D.A. “Dielectric Spectroscopy of Colloidal Suspensions”, J. Colloid and Interface Sci., 131, 2, 448-460 (1988)
- Rose, L.A., Baygents, J.C. and Saville, D.A. “The Interpretation of Dielectric Response Measurements on Colloidal Dispersions using dynamic Stern Layer Model”, J. Chem. Phys., 98, 5, 4183-4187 (1992)
- Maxwell, J.C. “Electricity and Magnetism”, Vol.1, Clarendon Press, Oxford (1892)
- Wagner, K.W., Arch. Elektrotech., 2, 371 (1914)
- O’Konski, C.T., “Electric Properties of Macromolecules v. Theory of Ionic Polarization in Polyelectrolytes”, J. Phys. Chem, 64, 5, 605-612 (1960)
- Bruggeman, D.A.G., Annln Phys., 24, 636 (1935)
- DeLacey, E.H.B. and White, L.R., “Dielectric Response and Conductivity of Dilute Suspensions of Colloidal Particles”, J. Chem. Soc. Faraday Trans., 77, 2, 2007 (1982)
- Dukhin, S.S. and Shilov V.N. “Dielectric phenomena and the double layer in dispersed systems and polyelectrolytes”, John Wiley and Sons, NY, (1974)
- Derjaguin , B.V. and Landau, L., “Theory of the stability of strongly charged lyophobic sols and the adhesion of strongly charged particles in solution of electrolytes”, Acta Phys. Chim, USSR, 14, 733 (1941)
- Verwey, E.J.W. and Overbeek, J.Th.G., “Theory of the Stability of Lyophobic Colloids”, Elsevier (1948)
- Liftshitz, E.M., “Theory of molecular attractive forces”, Soviet Phys. JETP 2, 73 (1956)
- Derjaguin, B.V. and Muller, V.M. “Slow coagulation of hydrophobic colloids”, Dokl. Akad. Nauk SSSR, 176, 738-741 (1967)
- Marlow, B.J. and Rowell, R.L. “Electrophoretic Fingerprinting of a Single Acid Site Polymer Colloid Latex”, Langmuir, 7, 2970-2980 (1991)
- Marlow, B.J, Fairhurst, D. and Schutt, W. “Electrophoretic Fingerprinting an the Biological Activity of Colloidal Indicators”, Langmuir, 4, 776 (1988)
- Goodwin, J.W., Gregory, T., and Stile, J.A. “A Study of Some of the Rheological Properties of Concentrated Polystyrene Latices”, Adv. In Colloid and Interface Sci., 17, 185-195, (1982)
- Probstein, R,F., Sengun, M.R., and Tseng, T.C., “Bimodal model of concentrated suspension viscosity for distributed particle sizes”, J. Rheology, 38, 4, 811-828, (1994)
- Russel, W.B., Saville, D.A. and Schowalter, W.R. “Colloidal Dispersions”, Cambridge University Press, (1989)
- Kamphuis, H., R.J.J.Jongschaap and P.F.Mijnlieff, “A transient-network model describing the rheological behavior of concentrated dispersions”, Rheological Acta, 23, 329-344, (1984)
- Ferry, J.D., Sawyer, W.M., and Ashworth, J.N., “Behavior of Concentrated polymer Solutions under Periodic Stresses”, J. of Polymer Sci., 2, 6, 593-611, (1947)
- T.G.M. van de Ven and Mason, S.G., “The microrheology of colloidal dispersions”, J. Colloid Interface Sci., 57, 505 (1976)
- T.G.M. van de Ven, “Colloidal Hydrodynamics”, Academic Press, (1989)
- Happel J. and Brenner, H, “Low Reynolds Number Hydrodynamics”, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, (1973)
- Happel J., “Viscous flow in multiparticle systems: Slow motion of fluids relative to beds of spherical particles”, AICHE J., 4, 197-201 (1958)
- Kuwabara, S. “The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers”, J. Phys. Soc. Japan, 14, 527-532 (1959)
- Kruyt, H.R. “Colloid Science”, Elsevier: Volume 1, Irreversible systems, (1952)
- Dukhin, A.S. and Goetz, P.J. “Acoustic Spectroscopy for Concentrated Polydisperse Colloids with High Density Contrast”, Langmuir, 12 [21] 4987-4997 (1996)
- Dukhin, A.S. and Goetz, P.J. “New Developments in Acoustic and Electroacoustic Spectroscopy for Characterizing Concentrated Dispersions”, Colloids and Surfaces, 192, 267-306 (2001)
- Brinkman, H.C. “A calculation of viscous force exerting by a flowing fluid on a dense swarm of particles”, Appl. Sci. Res., A1, 27 (1947)
- Li, Yongcheng., Park, C.W. “Effective medium approximation and deposition of colloidal particles in fibrous and granular media”, Adv. In Colloid and Interface Sci., 87, 1-74 (2000)
- Christoforou, C.C., Westermann-Clark, G.B. and J.L.Anderson, “The Streaming Potential and Inadequacies of the Helmholtz Equation”, J. Colloid and Interface Science, 106, 1, 1-11 (1985)
- Gonzalez-Fernandez, C.F., Espinosa-Jimenez, M., Gonzalez-Caballero, F. “The effect of packing density cellulose plugs on streaming potential phenomena”, Colloid and Polymer Sci., 261, 688-693 (1983)
- Hidalgo-Alvarez, R., de las Nieves, F.J., Pardo, G., “Comparative Sedimentation and Streaming Potential Studies for z -potential Determination”, J. Colloid and Interface Sci., 107, 2, 295-300 (1985)
- Groves, J. and Sears, A. “Alternating Streaming Current Measurements”, J. Colloid and Interface Sci., 53, 1, 83-89 (1975)
- Chowdian, P., Wassan, D.T., Gidaspow, D., “On the interpretation of streaming potential data in nonaqueous media”, Colloids and Surfaces, 7, 291-299 (1983)
- Smoluchowski, M., in Handbuch der Electrizitat und des Magnetismus”, vol.2, Barth, Leipzig (1921).
- O’Brien, R.W. and White, L.R. “Electrophoretic mobility of a spherical colloidal particle”, J. Chem. Soc. Faraday Trans., II, 74, 1607-1624 (1978)
- Dukhin, S.S. and Semenikhin, N.M. “Theory of double layer polarization and its effect on the electrokinetic and electrooptical phenomena and the dielectric constant of dispersed systems”, Kolloid. Zh., 32, 360-368 (1970)
- Midmore, B.R. and Hunter, R.J., J. Colloid Interface Science, 122, 521 (1988)
- O’Brien, R.W., “The solution of electrokinetic equations for colloidal particles with thin double layers”, J. Colloid Interface Sci, 92, 204-216 (1983)
- O’Brien, R.W. “Electroosmosis in Porous Materials”, Journal of Colloid and Interface Science”, 110, 2, 477-487 (1986)
- Dukhin, A. S., Shilov, V.N. and Borkovskaya Yu. “Dynamic Electrophoretic Mobility in Concentrated Dispersed Systems. Cell Model.”, Langmuir, 15, 10, 3452-3457 (1999)
- Zukoski, C.F. and Saville, D.A. “Electrokinetic properties of particles in concentrated suspensions”, J. Colloid Interface Sci., 115, 422-436 (1987)
- Hunter, R.J. “Zeta potential in Colloid Science”, Academic Press, NY (1981)
- Levine, S. and Neale, G.H. “The Prediction of Electrokinetic Phenomena within Multiparticle Systems.1.Electrophoresis and Electroosmosis.”, J. of Colloid and Interface Sci., 47, 520-532 (1974)
- Kozak M.W. and Davis, J.E. “Electrokinetic phenomena in Fibrous Porous Media”, Journal of Colloid and Interface Science, 112, 2, 403-411 (1986)
- Smith, K.L., and Fuller, G.G., “Electric Field Induced Structure in Dense Suspensions”, J. of Colloid and Interface Sci., 155, 1, 183-190, (1993)
- Marshall, L., Goodwin, J.W., and Zukoski, C.F., “The effect of Electric Fields on the Rheology of Concentrated Suspensions”, J.Chem.Soc., Faraday Trans., (1988)
- Murtsovkin, V.A. and Muller, V.M. “Steady-State Flows Induced by Oscillations of a Drop with an Adsorption Layer”, J. of Colloid and Interface Sci., 151, 1, 150-156, (1992)
- Murtsovkin, V.A. and Muller, V.M. “Inertial Hydrodynamic Effects in Electrophoresis of Particles in an Alternating Electric Field”, J. of Colloid and Interface Sci., 160, 2, 338-346 (1993)
- Malkin, E. S. ; Dukhin, A. S. “Interaction of Dispersed Particles in an Electric Fields and Linear Concentration Polarization of the Double Layer”, Kolloid. Zh., 5, 801-810, (1982)
- Dukhin, A. S. ; Murtsovkin, V. A. “Pair Interaction of Particles in Electric Field. 2. influence of Polarization of Double Layer of Dielectric Particles on their Hydrodynamic Interaction in Stationary Electric Field”, Kolloid. Zh., 2, 203-209, (1986)
- Gamayunov, N.I., Murtsovkin, V.A. and Dukhin, A.S. “Pair interaction of particles in electric field. Features of hydrodynamic interaction of polarized particles”, Kolloid. Zh., 48, 2, 197-209 (1986)
- Estrela-L’opis, V.R, Dukhin, S.S. and Shilov, V.N., Kolloid. Zh., 36, 6, 1140 (1974)
- Shilov, V.N. and Estrela-L’opis, V.R., in “Surface forces in Thin Films” , ed.B.V.Derjaguin, Nauka, Moskow, p.39 (1979)
- Andreson, J. and oth. Langmuir, 16, 9208-9216 (2000)
- Ulberg, Z. R. ; Dukhin, A. S. “Electrodiffusiophoresis- Film Formation in AC and DC Electrical Fields and Its Application for Bactericidal Coatings”, Progress in Organic Coatings, 1, 1-41, (1990)
- Bohren, C. and Huffman, D. “absorption and Scattering of Light by Small Particles”, J. Wiley & Sons, 530 p., (1983)
- Bruno Rossi, “Optics”, Addison-Wesley, Reading, MA, 510 p, (1957).
- Chu, B., and Liu, T. “Characterization of nanoparticles by scattering techniques”, J. of Nanoparticle Research, 2, 29-41, (2000)
- Phillips, D.L. “A Technique for the Numerical Solution of Certain Integral Equations of the First Kind”, J. Assoc. Comput. Mach., 9, 1, 84-97 (1962)
- Twomey, S. “On the Numerical Solution of Fredholm Integral Equation of the First Kind by the Inversion of the Linear System Produced by Quadrature”, J. Assoc. Comput. Mach., 10, 1, 97-101 (1963)
- Fisker, R., Carstensen, J.M., Hansen, M.F., Bodker, F. and Morup, S., “Estimation of nanoparticle size distribution by image analysis”, J. of Nanoparticle Research, 2, 267-277 (2000)
- Heywood, H, “The origins and development of Particle Size Analysis”, in “Particle size analysis”, ed. Groves, M.J and oth., The Society for analytical chemistry, London, (1970)
- Allen, T., “Particle size measurement”, 4th edition, Chapman and Hall, NY, (1990)
- Allen, T. “Sedimentation methods of particle size measurement”, Plenary lecture presented at PSA’85 (ed. P.J. Llloyd), Wiley, NY (1985)
- Mie, G., “Beitrage zur Optik truber Medien speziell kolloidaler Metallosungen”, Ann Phys., 25, 377-445 (1908)
- Tsai, W.C. and Pogorzelski, R.J. “Eigenfunction solution of the scattering of beam radiation fields by spherical objects”, J. Opt. Soc. Am, 65, 1457-1463 (1975)
- Hackley, V.A. and Ferraris, C.F. “The Use of Nomenclature in Dispersion Science and Technology”, NIST, special publication 960-3 (2001)
- Anson, L.W. and Chivers, R.C. “Thermal effects in the attenuation of ultrasound in dilute suspensions for low values of acoustic radius”, Ultrasonic, 28, 16-25 (1990)
- Kosmulski, M. and Rosenholm, J.B. “Electroacoustic study of adsorption of ions on anatase and zirconia from very concentrated electrolytes”, J. Phys. Chem., 100, 28, 11681-11687 (1996)
- Kosmulski, M. “Positive electrokinetic charge on silica in the presence of chlorides”, JCIS, 208, 543-545 (1998)
- Kosmulski, M., Gustafsson, J. and Rosenholm, J.B. “Correlation between the Zeta potential and Rheological properties of Anatase dispersions”, JCIS, 209, 200-206 (1999)
- Kosmulski, M., Durand-Vidal, S., Gustafsson, J. and Rosenholm, J.B. “Charge interactions in semi-concentrated Titania suspensions at very high ionic strength”, Colloids and Surfaces A, 157, 245-259 (1999)
- Deinega, Yu.F., Polyakova, V.M., Alexandrove, L.N. “Electrophoretic mobility of particles in concentrated electrolyte solutions”, Kolloid. Zh., 48, 3, 546-548 (1982)
- Dukhin, S.S., Churaev, N.V., Shilov, V.N. and Starov, V.M. “Problems of the reverse osmosis modeling”, Uspehi Himii, (Russian) 43, 6 , 1010-1023 (1988), English, 43, 6 (1988).
- Alekseev, O.L., Boiko, Yu.P., Ovcharenko, F.D., Shilov, V.N., Chubirka, L.A. “Electroosmosis and some properties of the boundary layers of bounded water”, Kolloid. Zh., 50, 2, 211-216 (1988)
- Rowlands, W.N., O’Brien, R.W., Hunter, R.J., Patrick, V. “Surface properties of aluminum hydroxide at high salt concentration”, JCIS, 188, 325-335 (1997).
- Ohshima, H. “A simple expression for Henry’s function for retardation effect in electrophoresis of spherical colloidal particles”, JCIS, 168, 269-271 (1994)
- Tian Hao, “Electrorheological fluids”, Adv. Materials, 13, 24, 1847-1857 (2001)
- Dukhin, A.S. and Goetz, P.J. “Ultrasound for characterizing colloids”, Elsevier, 2002
Streaming Current isochoric and non-isochoric. Seismoelectric effect
Steaming potential and streaming current occur in porous bodies when liquid is being pumped through them. These electrokinetic phenomena have been known for almost 200 years. It is widely used for studying zeta potential in porous bodies. The main field of application so far is in the paper industry. Streaming potential is usually the preferred way of performing this measurement. However, the streaming current method does not require conductivity for calculating zeta potential, which presents a certain advantage.
One of the important areas of the streaming current and streaming potential application is seismoelectric effect . This phenomenon occurs in underground rocks when sound waves propagate through. This seismoelectric effect is widely used for characterizing underground formations with regard to water or oil presence.
Our DT-300 zeta potential probe is suitable for characterizing streaming current in cores at high frequency of 3 MHz. It can be very useful for measuring zeta potential of cores and predicting of wettability of porous bodies. It also offers possibility of modeling seismoelectric effect in laboratory conditions and single frequency. This dramatically simplifies theory verification and modeling.
Streaming potential and streaming current are also used for monitoring and quality control of chromatographic resins. Zeta potential of the pores controls interaction of these resins with proteins. That is why detail information of the resin zeta potential allows optimization of protein treatment.
Another application of our method for streaming current measurement is study of the structure in carbon nano-tubes dispersions. It turns out that phase of streaming current is very sensitive to the strength of the carbon nano-tube’s structure.
REFERENCES:
1.Frenkel J. “On the Theory of Seismic and Seismoelectric Phenomena in a Moist Soil”, re-published, J. Engineering Mechanics, 131, 9, pp. 879-887 (2005).
2.Dukhin, A.S., Goetz, P.J. and Thommes M. “Seismoelectric effect: non-isochoric Streaming Current. 1. Experiment”, JCIS, (2010)
3. Dukhin, A.S., and Shilov, V.N. “Seismoelectric effect: non-isochoric Streaming Current. 2. Theory and experimental verification”, JCIS, (2010)
Longitudinal rheology. Bulk Viscosity and Longitudinal Viscosity
Propagation of a longitudinal stress wave through a visco-elastic media creates dissipation of mechanical energy, similarly to a shear stress wave. The rate of dissipation depends on two parameters: bulk viscosity and longitudinal viscosity. For Newtonian liquid it is bulk viscosity that is analog to the dynamic viscosity for the shear stress. For non-Newtonian liquid it is longitudinal viscosity, analog to the shear viscosity for the shear rheology.
Measurement of ultrasound attenuation is the only known way of characterizing these parameters for both Newtonian and non-Newtonian liquids. Our Acoustic sensor allows very precise measurement of the ultrasound attenuation. It is important to perform this measurement at different frequencies. Frequency dependences allow resolving between bulk viscosity and longitudinal viscosity.
Bulk viscosity is important for verification of molecular theories of Newtonian liquids. We published a paper that reports the value of this parameter for 12 different Newtonian liquids. This paper describes methodology of such study. It can be simply reproduced with any other Newtonian liquid. We show that bulk viscosity is an independent property of liquid with practically no correlation with other parameters, such as dynamic viscosity, dielectric permittivity, or compressibility.
Longitudinal viscosity yields information about relaxation times in non-Newtonian liquids at MHz range. These high frequencies are not accessible with traditional shear rheology. That is why longitudinal rheology is complimentary to the traditional shear rheology. Longitudinal frequency spectra can be used similarly to the shear viscosity – shear rate dependence, but at much higher frequencies.
One of the important advantages of our longitudinal rheology measurement is ability to use it online for continuous non-destructive monitoring of the industrial process. This function is much harder to implement with traditional shear rheology.
Short introduction to electro acoustic theory
Electroacoustic effects are result of coupling between acoustic and electric fields. Debye realized 70 years ago [1] that in the presence of a longitudinal sound wave, any differences in the effective mass or friction coefficient between anions and cations would result in different displacement amplitudes. In turn, this difference in displacement would create an alternating electric potential between points within the solution. Indeed, this phenomenon is measurable and can yield useful information about the properties of ions. It is usually referred to as an “Ion Vibration Potential” (IVP). It was used for measuring sizes of ions in 60th. Sadly, this phenomenon has been largely forgotten, and virtually all of the interest in electroacoustic phenomena has shifted from pure electrolyte solutions to colloids
However, the first electroacoustic theory was developed for a third class of systems – porous bodies, in 1944 by Frenkel [2]. He created theory of electroseismic effect using Smoluchowski theory as a starting point. We use this effect now for studying porous bodies with DT-300 Zeta Potential probe.
First electroacoustic measurements in colloids were performed by Hermans [3] and Rutgers [4] in 1938. Enderby and Booth [5,6] developed the first theory for CVP in the early 1950’s.
Detail historical review of all developments on the field of electroacoustics can be found in our book [7].
Here we present just one very useful expression for Colloid Vibration Current derived by V. Shilov and oth. [8]using a well-known Onsager reciprocal relationship for Smoluchwski type electrokinetic theory:
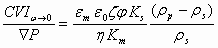
where ε is dielectric permittivity, η is viscosity, ρ is density, φ is volume fraction, ζ is zeta potential. Index p corresponds to particle, m to media, s to the system in whole.
This equation is very useful for estimating trend of electroacoustic change depending on various parameters. It is valid quantitatively for submicron particles with sizes under 300 nm with thin double layer and negligible surface conductivity. Double layers must be not overlapped, which somewhat restricts volume fraction for a given particle size.
REFERENCES.
-
-
Debye, P. “A method for the determination of the mass of electrolyte ions”, J. Chem. Phys., 1,13-16, (1933)
-
Frenkel J. “On the Theory of Seismic and Seismoelectric Phenomena in a Moist Soil”, re-published, J. Engineering Mechanics, 131, 9, pp. 879-887 (2005).
-
Hermans, J., Philos. Mag., 25, 426 (1938)
-
Rutgers, A.J. and Rigole, W. “Ultrasonic vibration potentials in colloid solutions, in solutions of electrolytes and pure liquids”, Trans. Faraday Soc., 54, 139-143 (1958)
-
Enderby, J.A. “On Electrical Effects Due to Sound Waves in Colloidal Suspensions”, Proc. Roy. Soc., London, A207, 329-342 (1951)
-
Booth, F. and Enderby, J. “On Electrical Effects due to Sound Waves in Colloidal Suspensions”, Proc. of Amer. Phys. Soc., 208A, 32 (1952)
-
Dukhin A.S. and Goetz, P.J. “Ultrasound for characterizing colloids”, Elsevier, 2002
-
Dukhin, A.S., Shilov, V.N, Ohshima, H., Goetz, P.J “Electroacoustics Phenomena in Concentrated Dispersions. New Theory and CVI Experiment”, Langmuir, 15, 20, 6692-6706, (1999)
-
